Cell vectors are passed correctly
PLUMED must receive the cell vectors from the MD code in order to calculate CVs correctly.
To test that cell vectors are passed correctly to PLUMED we run a short trajectory and output the cell vectors
that are passed to PLUMED using the following command:
c: CELLGet the components of the simulation cell More details
Trajectory
Input and output files for the test calculation are available inthis zip archive
Results
| MD code output | PLUMED output | Tolerance | % Difference |
|---|---|---|---|
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0012 & 0.0000 & 0.0000 \\ 0.0000 & 0.0012 & 0.0000 \\ 0.0000 & 0.0000 & 0.0012 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0012 & 0.0000 & 0.0000 \\ 0.0000 & 0.0012 & 0.0000 \\ 0.0000 & 0.0000 & 0.0012 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0405 & 0.0000 & 0.0000 \\ 0.0000 & 0.0405 & 0.0000 \\ 0.0000 & 0.0000 & 0.0405 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0405 & 0.0000 & 0.0000 \\ 0.0000 & 0.0405 & 0.0000 \\ 0.0000 & 0.0000 & 0.0405 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0405 & 0.0000 & 0.0000 \\ 0.0000 & 0.0405 & 0.0000 \\ 0.0000 & 0.0000 & 0.0405 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0405 & 0.0000 & 0.0000 \\ 0.0000 & 0.0405 & 0.0000 \\ 0.0000 & 0.0000 & 0.0405 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0405 & 0.0000 & 0.0000 \\ 0.0000 & 0.0405 & 0.0000 \\ 0.0000 & 0.0000 & 0.0405 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0050 & 0.0000 & 0.0000 \\ 0.0000 & 0.0050 & 0.0000 \\ 0.0000 & 0.0000 & 0.0050 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0050 & 0.0000 & 0.0000 \\ 0.0000 & 0.0050 & 0.0000 \\ 0.0000 & 0.0000 & 0.0050 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0050 & 0.0000 & 0.0000 \\ 0.0000 & 0.0050 & 0.0000 \\ 0.0000 & 0.0000 & 0.0050 \end{array}$ |
| $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 2.2660 & 0.0000 & 0.0000 \\ 0.0000 & 2.2660 & 0.0000 \\ 0.0000 & 0.0000 & 2.2660 \end{array}$ | $\begin{array}{ccc} 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \\ 0.0010 & 0.0010 & 0.0010 \end{array}$ | $\begin{array}{ccc} 0.0050 & 0.0000 & 0.0000 \\ 0.0000 & 0.0050 & 0.0000 \\ 0.0000 & 0.0000 & 0.0050 \end{array}$ |
The table below includes some of the results from the calculation. The columns contain:
- The values for the cell vectors that were obtained from the MD code, $x_{md}$.
- The values for the cell vectors that were obtained from PLUMED, $x_{pl}$.
- The tolerances that were used when comparing these quantities, $\delta$.
- The values of $100\frac{\vert x_{md} - x_{pl}\vert }{ \delta }$.
If the PLUMED interface is working correctly the first two sets of numbers should be identical and the final column should be filled with zeros.
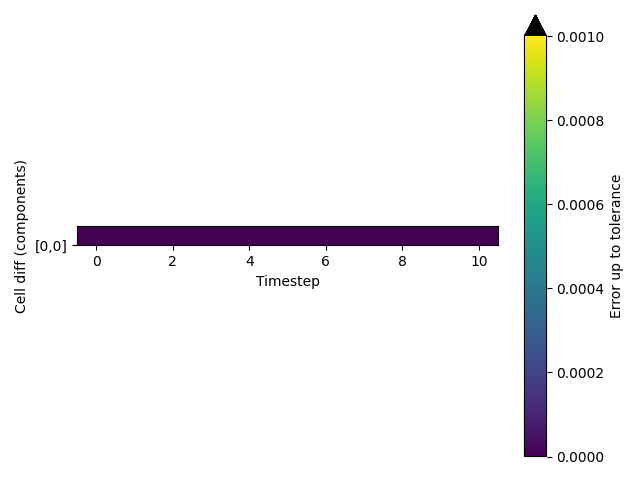
Graphical representation (beta)
A visualization of the table above: